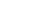Angewandte Informatik
Aufgabe Kryptografie 3
1. Schritt: Alice und Bob einigen sich gemeinsam auf eine Primzahl p und eine Zahl g zwischen 1 und p − 1:
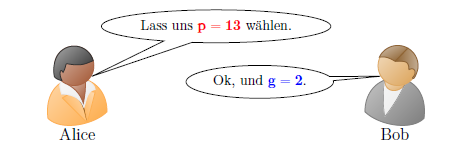
2. Schritt: beide überlegen sich geheim eine Zufallszahl:
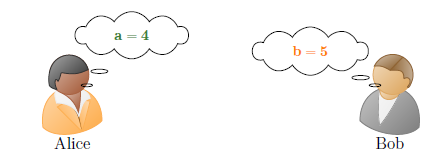
3. Schritt: Alice berechnet A=g a mod p und Bob berechnet B=gb mod p:
4. Schritt: Diese im geheimen mit der Modulo-Funktion errechneten Zahlen tauschen sich Alice und Bob jetzt aus:
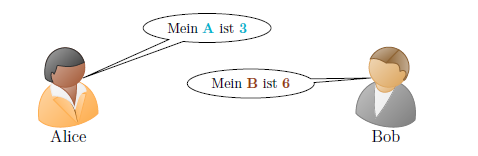
5. Schritt: Nun wird der gemeinsame geheime Schlüssel k berechnet. Dafür benutzt Alice das B von Bob und berechnet k = B a mod p und Bob benutzt das A von Alice und berechnet k = A b mod p:
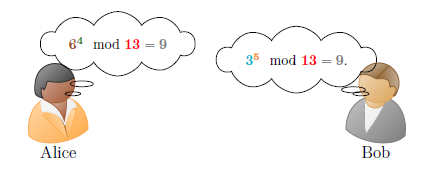
Alice und Bob haben nun die gleiche Zahl berechnet und können k = 9 als gemeinsamen geheimen Schlüssel benutzen. Ein Angreifer kennt nur p, g, A und B, da diese Zahlen NICHT geheim getauscht wurden. Ohne das Wissen über a und b helfen die „erbeuteten“ Zahlen aber nichts. In der Praxis ist dieses Verfahren nach Diffie und Hellman benannt und wird mit deutlich größeren Zahlen umgesetzt, damit ein Angreifer den Schlüssel nicht einfach erraten kann. So kann die Primzahl p durchaus mal 500 Dezimalstellen haben.